2. Zadania do powtórzenia w dniach 27.04-29.04.2020
1. Określ zbiór wartości i przedziały monotoniczności funkcji
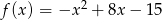 .
. Odp. Zbiór wartości:
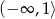 , rosnąca na
, rosnąca na 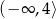 , malejąca na
, malejąca na 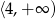
2. Wyznacz najmniejszą i największą wartość funkcji
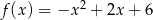 w przedziale
w przedziale 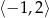 .
. Odp.
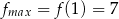 ,
, 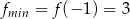
3. Sprowadź do postaci ogólnej funkcję kwadratową
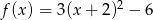 .
. Odp. y=
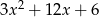
4. Funkcja kwadratowa
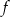 przyjmuje największą wartość równą
przyjmuje największą wartość równą 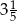 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 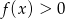 jest przedział
jest przedział 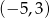 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 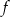 w postaci ogólnej.
w postaci ogólnej. Odp.
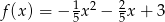
5. Funkcja kwadratowa
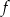 jest określona dla wszystkich liczb rzeczywistych
jest określona dla wszystkich liczb rzeczywistych  wzorem
wzorem 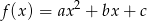 . Największa wartość funkcji
. Największa wartość funkcji 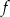 jest równa 6 oraz
jest równa 6 oraz 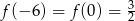 . Oblicz wartość współczynnika
. Oblicz wartość współczynnika  .
. Odp.
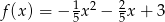
6. Jedynym miejscem zerowym funkcji kwadratowej
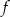 jest liczba 2. Wykres funkcji
jest liczba 2. Wykres funkcji 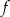 przecina oś
przecina oś 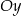 w punkcie o współrzędnych
w punkcie o współrzędnych 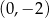 . Wyznacz wzór tej funkcji w postaci ogólnej.
. Wyznacz wzór tej funkcji w postaci ogólnej. Odp. y=
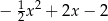
7. Funkcja kwadratowa
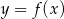 przyjmuje wartości ujemne tylko dla
przyjmuje wartości ujemne tylko dla 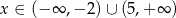 , a jej zbiorem wartości jest przedział
, a jej zbiorem wartości jest przedział 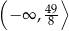 . Zapisz wzór funkcji kwadratowej
. Zapisz wzór funkcji kwadratowej 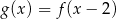 w postaci ogólnej.
w postaci ogólnej. Odp.
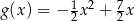
8. Wykresem funkcji kwadratowej
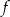 określonej wzorem
określonej wzorem 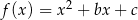 jest parabola, na której leży punkt
jest parabola, na której leży punkt 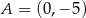 . Osią symetrii tej paraboli jest prosta o równaniu
. Osią symetrii tej paraboli jest prosta o równaniu 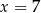 . Oblicz wartości współczynników
. Oblicz wartości współczynników 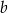 i
i  .
. Odp.
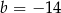 i
i 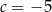
9. Dwóch braci pokonuje drogę z domu do szkoły pieszo. Młodszy potrzebuje na przebycie tej trasy 30 minut, a starszy 20 minut. Po ilu minutach starszy brat dogoni młodszego, jeśli wyjdzie z domu 5 minut po nim?
Odp. Po 10 minutach
10. Zawodnik kopnął piłkę, która zakreśliła w powietrzu fragment toru opisanego równaniem
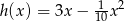 (
( oznacza poziomą odległość piłki od zawodnika, a
oznacza poziomą odległość piłki od zawodnika, a 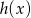 wysokość na jakiej znajduje się piłka). Oblicz, na jaką największą wysokość wzniosła się piłka.
wysokość na jakiej znajduje się piłka). Oblicz, na jaką największą wysokość wzniosła się piłka.Odp. 22,5
11. Doświadczalnie ustalono, że czas
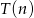 , liczony w sekundach, potrzebny na alfabetyczne ułożenie
, liczony w sekundach, potrzebny na alfabetyczne ułożenie  kartek z nazwiskami wyraża się, z dobrym przybliżeniem, wzorem
kartek z nazwiskami wyraża się, z dobrym przybliżeniem, wzorem 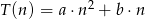 . Ułożenie 10 kartek trwa średnio 20 sekund, a 30 kartek średnio 90 sekund. Wyznacz wzór funkcji
. Ułożenie 10 kartek trwa średnio 20 sekund, a 30 kartek średnio 90 sekund. Wyznacz wzór funkcji 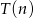 i oblicz, ile kartek można ułożyć średnio w ciągu 50 sekund.
i oblicz, ile kartek można ułożyć średnio w ciągu 50 sekund. Odp.
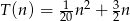 ,
, 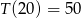
12. Z krawędzi dachu podrzucono kamień, który po 2 sekundach spadł na ziemię. Wysokość (wyrażoną w metrach), na jakiej znajdował się kamień nad ziemią po upływie
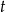 sekund od chwili jego podrzucenia, opisuje funkcja
sekund od chwili jego podrzucenia, opisuje funkcja 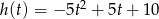 , gdzie
, gdzie 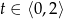 .
. - Podaj, z jakiej wysokości (od ziemi) kamień został podrzucony.
- Oblicz, po jakim czasie od momentu podrzucenia kamień osiągnął największą wysokość.
- Oblicz największą wysokość (od ziemi), na jaką wzniósł się ten kamień.
Odp. a) 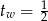 , b)
, b) 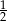 s, c)
s, c) 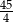 m
m
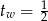 , b)
, b) 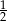 s, c)
s, c) 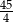 m
m
13. Dziedziną funkcji 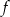 określonej wzorem
określonej wzorem 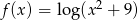 jest zbiór
jest zbiór
A)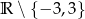 B)
B) 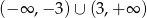 C)
C) 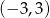 D)
D) 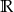
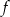 określonej wzorem
określonej wzorem 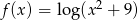 jest zbiór
jest zbiórA)
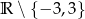 B)
B) 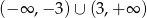 C)
C) 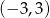 D)
D) 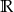
14. Do dziedziny funkcji 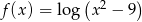 nie należy liczba
nie należy liczba
A) -5 B)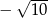 C)
C) 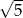 D) 6
D) 6
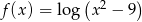 nie należy liczba
nie należy liczbaA) -5 B)
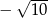 C)
C) 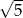 D) 6
D) 6
15. Funkcja wykładnicza 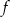 określona wzorem
określona wzorem 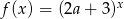 jest malejąca dla
jest malejąca dla
A)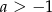 B)
B) 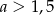 C)
C) 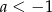 D)
D) 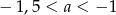
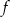 określona wzorem
określona wzorem 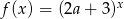 jest malejąca dla
jest malejąca dlaA)
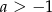 B)
B) 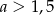 C)
C) 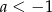 D)
D) 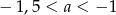
16. Wartością funkcji 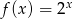 jest liczba
jest liczba
A) -8 B) -4 C) 0 D) 3
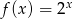 jest liczba
jest liczbaA) -8 B) -4 C) 0 D) 3
17. Funkcja 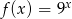 dla argumentu
dla argumentu 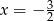 przyjmuje wartość
przyjmuje wartość
A)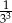 B) 27 C)
B) 27 C) 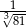 D)
D) 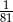
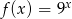 dla argumentu
dla argumentu 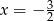 przyjmuje wartość
przyjmuje wartość A)
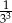 B) 27 C)
B) 27 C) 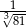 D)
D) 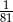
18. Wskaż zbiór, w którym funkcja 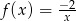 jest rosnąca.
jest rosnąca.
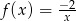 jest rosnąca.
jest rosnąca.
A) 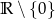 B)
B) 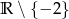 C)
C) 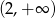 D)
D) 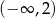
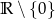 B)
B) 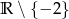 C)
C) 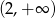 D)
D) 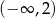
19. Dana jest funkcja określona wzorem 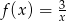 . Wartość tej funkcji w punkcie
. Wartość tej funkcji w punkcie 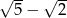 jest równa
jest równa
A)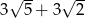 B)
B) 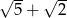 C)
C) 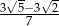 D)
D) 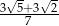
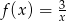 . Wartość tej funkcji w punkcie
. Wartość tej funkcji w punkcie 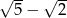 jest równa
jest równaA)
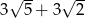 B)
B) 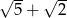 C)
C) 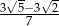 D)
D) 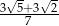
20. Wskaż zbiór wartości funkcji 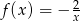 .
.
A)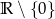 B)
B) 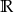 C)
C) 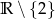 D)
D) 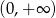
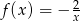 .
. A)
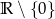 B)
B) 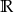 C)
C) 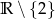 D)
D) 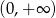
21. Punkt o współrzędnych 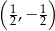 należy do wykresu funkcji logarytmicznej opisanej wzorem
należy do wykresu funkcji logarytmicznej opisanej wzorem
A)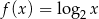 B)
B) 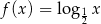 C)
C) 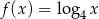 D)
D) 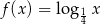
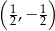 należy do wykresu funkcji logarytmicznej opisanej wzorem
należy do wykresu funkcji logarytmicznej opisanej wzorem A)
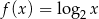 B)
B) 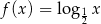 C)
C) 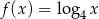 D)
D) 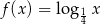
21. Do wykresu funkcji 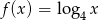 nie należy punkt
nie należy punkt
A)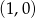 B)
B) 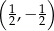 C)
C) 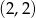 D)
D) 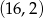
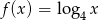 nie należy punkt
nie należy punktA)
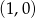 B)
B) 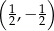 C)
C) 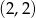 D)
D) 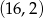
22. Na rysunku przedstawiono fragment wykresu funkcji wykładniczej 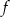 określonej wzorem
określonej wzorem 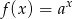 . Punkt
. Punkt 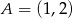 należy do tego wykresu funkcji.
należy do tego wykresu funkcji.
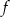 określonej wzorem
określonej wzorem 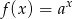 . Punkt
. Punkt 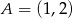 należy do tego wykresu funkcji.
należy do tego wykresu funkcji. 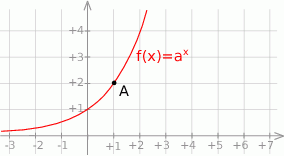
Podstawa  potęgi jest równa
potęgi jest równa
A)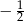 B)
B) 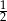 C)
C) 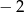 D) 2
D) 2
 potęgi jest równa
potęgi jest równaA)
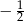 B)
B) 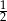 C)
C) 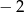 D) 2
D) 2
23. Jeżeli do wykresu funkcji wykładniczej 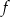 należy punkt
należy punkt 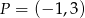 , to funkcja ta określona jest wzorem
, to funkcja ta określona jest wzorem
A)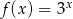 B)
B) 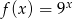 C)
C) 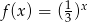 D)
D) 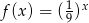
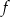 należy punkt
należy punkt 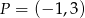 , to funkcja ta określona jest wzorem
, to funkcja ta określona jest wzoremA)
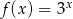 B)
B) 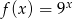 C)
C) 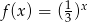 D)
D) 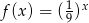
Brak komentarzy:
Prześlij komentarz